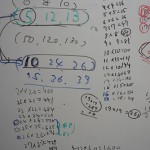福西です。この日は、その頃ちまたで話題になっていたABC予想に寄せて、ピタゴラス数を探しました。4年生のクラスでも取り上げた問題ですが、5年生ならばどのように考えてくれるだろうかと期待しました。
(かなりのところまで法則性を突き止めました)
問い
ピタゴラス数を探せ。
ピタゴラス数というのは、三平方の定理a^2+b^2=c^2を満たす自然数解(a,b,c)のことです。たとえば(3,4,5)がその一つです。3^3=9、4^2=16、5^2=25。9+16=25。このような「ピッタリカンカン数」を探せという問題です。(ちなみに3、4、5は、直角三角形の3辺の長さに相当します)
手始めに、おなじみの九九の表を作ってもらいました。ただし対角成分のみで、1×1=1、2×2=4、…、9×9=81の9つです。このような数を「平方数」といいます。(平方は正方形のことです)。さらに5年生なので、そのあと最低でも、20×20まで(結局もっと計算したいということで、30×30まで)それを実行してもらいました。
(右側と左下にK君とTa君の書いた平方数があります。拡大すると見えますが、実際には20を通り越して30×30まで計算してくれました)
この中から、イコールの右側の2つの数を足して、またもう一つの数になっていれば(要するにこのリストの中にある数であれば)、それがピタゴラス数ということになります。そのように考えて、最初に(3,4,5)と(6,8,10)を見つけてくれました。(このクラスでは(6,8,10)が一番最初に見つかりました)。
そして、K君とTa君は、(3,4,5)と(6,8,10)、そして(30,40,50)も成り立つことを確かめた結果、(3,4,5)の3倍である(9,12,15)や、4倍である(12,16,20)もピタゴラス数ではないか? と推測してくれました。そして実際、それが成り立っていることを確かめました。
K君とTa君が見つけた解
(3,4,5)
(6,8,10)=(3,4,5)×2
(9,12,15)=(3,4,5)×3
(12,16,20)=(3,4,5)×4
…
(30,40,50)=(3,4,5)×10
…
一方、To君の考えてくれた平方数の列挙。列挙という事は、つまりこちらも法則を見つけてくれました。
To君の考えた道筋は、次のとおりです。
(5,12,13)は、12と13が1つ違い。そして次に左端の数が7の場合があるのではないかと予想し、頑張って計算をして、(7,24,25)を見つけてくれました。その発見に気をよくして、次に9の場合がないか探したところ、これが今度はなかなか見付かりません。それで、「うーん」となっていたところ、ふと1つ違いの平方数の「差」を取ることに気付いてくれました。
つまり、以下の平方数の並びの隣同士の差を取って、それが平方数になるところはないか? と探し始めました。これによって、作業がうんとはかどりました。
1:1
2:4 4-1=3
3:9 9-4=5
4:16 16-9=7
5:25 25-16=9
6:36 …
7:49
8:64
9:81
10:100
11:121
12:144
13:169
14:196
15:225
16:256
17:289
18:324
19:361
20:400
21:441
22:484
23:529
24:576
25:625
26:676
27:719
28:784
29:841
30:900
このような数字を眺めていたとき、また一つ気が付いたことがありました。それは、「差」が3,5,7,9,11,13,15…と、「2ずつ増えている」ことです。
ということは、差が49の次は…と考えると、(64は偶数だからなくて)、81に白羽の矢が立ちます。
81-49=32
32÷2=16、
つまり、(9,b,c)=(9,24+16,25+16)=(9,40,41)
が、ピタゴラス数ではないか? という予想が成り立ちます。実際確かめてみたところ、(もはや表にはない数の純然たる予想です!)
40^2=1600
41^2=1681 (この計算をした時点で、To君が「おっ!」と目を輝かせていました)
81+1600=1681 (成り立っています!)
そしてそれまでの結果を並べて書いてみて、それを眺めていたTo君が、さらなる発見を。
(3,4,5)
(5,12,13)
(7,24,25)
(9,40,41)
「これって、真ん中の数と、右の数が、どっちも+8、+12、+16…と、その差も4ずつ増えている!」
ということでした。その予想に従って、次に+20をしてみると、(11,52,53)が候補となりますが、実際に、
「おお! やっぱり!」
というTo君の歓声が聞かれました。
というわけで、To君は、先のK君とTa君の見つけた解のリストに、次のような新しい種類を追加してくれたのでした。
To君が見つけた解
(3,4,5)
(5,12,13)
(7,24,25)
(9,40,41)
…
(3+2+2+…、4+8+12+…、5+8+12+…)
そして、上の二つの結果を合わせると、かなり広範な解を見つけたことになります。
K君、Ta君、To君の発見したこと
(3,4,5)×n倍
(5,12,13)×n倍
(7,24,25)×n倍
(9,40,41)×n倍
…
(3+2+2+…、4+8+12+…、5+8+12+…)×n倍
(n=1,2,3…)
素晴らしい結果です!
さて、ここで問題です。
果たしてこれで、ピタゴラス数は「すべて」見付かったのでしょうか?
実は、そうではありません。これより以前に、Ta君が実際に上のリストには「ない」解を見つけてくれていました。
(Ta君の見つけた解)
そうです! (a,b,c)の「aが偶数」でかつn倍によって作られていないパターンは、今まで現われてきませんでした。
ここで、「aが偶数である」というだけならば、(3,4,5)を2倍とか10倍して作った(6,8,10)、(30,40,50)のような数がすでに見つかっています。しかし、(8,15,17)という組み合わせは、8なので、(4,b,c)という数がもとで、それを2倍したように見えますが、b,cにあたる数が分数になってしまいます。ということは、(8,15,17)は、いかなる解からもn倍して作られた数ではないことが分かります。Ta君、素晴らしい発見です!
でも、そんなの「ありえない」と思うかもしれません。しかし、実際に計算してみると、
64+225=289
17×17=289
となり、やはりこれもピタゴラス数の一つです。
ということは、ピタゴラス数は「まだまだ存在する」ということになります。