『かず』１〜２年 『中学・高校数学』 B 『高校数学』 A・Cクラス便り（2017年11月）

「山びこ通信」2017年度秋学期号より下記の記事を転載致します。

『かず』１〜２年 『中学・高校数学』 B 『高校数学』 A・C

担当 浅野 直樹

　かず１～２年クラスでは主に迷路を、その他のクラスでは中学数学や高校数学の内容に取り組んでいます。迷路と中学や高校の数学とは一見大きく異なりますが、かなり似たような頭の使い方をします。実例をご覧いただきましょう。

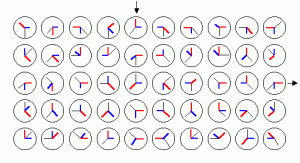
時計http://web.kyoto-inet.or.jp/people/eisaku/maze/clock.html 　より

左下の時計を(1, 1)、スタートを(5, 5)、ゴールを(10, 3) のように表記します。ゴールからたどると、(10, 3) → (10, 2) →(9, 3) → (8, 3) → (8, 2) → (9, 2) と進むしかないので、この道を確定させることができます。スタートからたどると、(5, 5) →(4, 4) → (4, 5) は行き止まりなので、(5, 5) → (6, 5) と最初の一歩を決めることができます。かず１～２年クラスの受講生たちの様子からしても、ゴールからの道をある程度確定させておくことがこの迷路を解くときのコツです。

m を5 以上の自然数とする。次の不等式が成り立つことを、数学的帰納法によって証明せよ。
m! > 2^m > m²
（長崎大）

先に答案を示します。

m! > 2^m > m² …① とする。

（I） m = 5 のとき
5! = 120, 2⁵ = 32,  5² = 25 より① は成り立つ。

（II） m = k （k > 5）のときに① が成り立つと仮定すると
k! > 2^k > k²

（ア）
（k + 1）! − 2^k+1
= （k + 1） ・ k! − 2 ・ 2^k
> （k + 1） ・ 2^k − 2 ・ 2^k
= （k − 1） ・ 2^k
> 0
よって、（k + 1）! > 2^k+1 が成り立つ。

（イ）
2^k+1 − （k + 1）²
= 2 ・ 2^k − （k² + 2k + 1）
> 2 ・ k² − k² − 2k − 1
= k² − 2k − 1
= （k − 1）² − 2
> 0 （k > 5 より（k − 1）² > 16 である）
よって、2^k+1 > （k + 1）² が成り立つ。

以上より、k + 1 のときも① が成り立つ。

以上より、m を5 以上の自然数とするとm! > 2^m > m² が成り立つ。

答案の本体である（II） では、使う条件とゴールが決まっているので、それらをしっかりと意識すれば式変形が見えてきます。
この２つの問題を同じ日に別のクラスで解いたので、受講生の年齢は大きく離れていても、同じような考え方をしていると強く感じたものです。