
福西です。
前回までの記録が抜けてしまってすみません。とりあえず今日の分を報告します。
Sちゃんとは先週から「クイーン問題」というのをしています。これは前にも考えたことがあるのですが、今回はより厳密に、回転して同じものは同一視することにした場合、何パターンあるかを考えました。Sちゃんとしているのは、クイーンが5個の場合です。
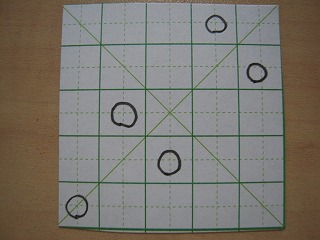
(5クイーン問題)
そこでSちゃんがどうやって重複を廃したかというと、以下のように考えたのでした。
「これまで考えてきたものはすべて、二本ある対角線のどこかにクイーンがいる。ということは、その対角線二本ともにクイーンがいないパターンはまだ考えていないので、それらがすべて新しいパターンとなる」
この発見はすごかったです。それでさらに2パターンが加わりました。これにはSちゃんも「やった」と歓声を上げていました。
その全部は、以下のようになります(すべてSちゃんが見つけた結果です)。もし根気のある方は、重複が無いかをチェックしてみて下さい(もしあるとすれば、それは私のタイプミスだと思います^^;)。
回転させてもクイーン(○)の配置がどこか異なっているということが条件です。それを見分ける判断材料として、1)中心 2)四隅 に、クイーンがあるかないかを見ることが役に立ちます。Sちゃんはこのことも駆使していました。
(1)
****○
**○**
○****
***○*
*○***
(2)
****○
*○***
**○**
***○*
○****
(3)
****○
○****
*○***
**○**
***○*
(4)
***○*
**○**
○****
*○***
****○
(5)
**○**
***○*
○****
*○***
****○
(6)
*○***
****○
**○**
***○*
○****
(7)
***○*
○****
**○**
*○***
****○
(8)
***○*
*○***
**○**
○****
****○
(9)
**○**
*○***
○****
****○
***○*
(10)
○****
*○***
***○*
**○**
****○
(11)
**○**
*○***
○****
***○*
****○
(12)
○****
*○***
**○**
***○*
****○
(13)
*○***
○****
**○**
****○
***○*
(14)
***○*
****○
**○**
*○***
○****
(15)
*○***
○****
***○*
**○**
****○
(16)
**○**
***○*
*○***
○****
****○
(17)
***○*
*○***
○****
**○**
****○
(18)
○****
***○*
*○***
**○**
****○
(19)
***○*
**○**
*○***
****○
○****
(20)二本の対角線上にクイーンがいないパターンその1
***○*
****○
○****
**○**
*○***
(21)二本の対角線上にクイーンがいないパターンその2
***○*
○****
****○
**○**
*○***
以上、21パターン!
さて、ここまでたどりついたわけですが、22パターン目はあるのでしょうか、それともないのでしょうか?? それが問題です。もしこれ以上なければ、いくら考えても出てこないわけですが、「これ以上ない!」ということを証明できれば、それはすごいことです。
小学校のうちは、答が最初から「ある」ものとして、「それは何でしょう?」という形で問題が出されますが、本当は答えがあるのかないのか分からないところから考えることが一番難しい、ということも話しました。またSちゃんならそれをできる人になれる、と言うと、照れ笑いしていました。
>本当は答えがあるのかないのか分からないところから考えることが一番難しい
そして「楽しい」という言葉も付け加えることができますね。正確には「苦しいけれども楽しい」といったところでしょうか。