
福西です。
1/21の記録です。
今日は、リクエストの『分数の巻』をしてもらいました。
特に、3/5=3÷5と、分数を割り算でも理解できることと、1=□/2=□/4=…としていく問題が重要でした。
そしてH君は、1/125を小数に直しなさいという問題では、迷わず
__
125)1
を実行していました。(これは先週した小数の割り算のおさらいです)
また、2-1/3=5/3という計算でも、暗黙のうちに2=6/3と変換していました。これができていればOKです。
今日も帰り際にまた、H君から「今度は、線図を書いて解く問題の巻を作ってきて~」とのリクエストがかかりました。ちょうど今学校で習っている箇所だそうです。ぜひ(^^)。ちなみに、~の巻というのは、このクラスでは10枚ほどのプリントを束にしたもののことで、男の子が好きそうな忍者を若干イメージしています。H君は、パズルの巻や扉の書も合わせると、かれこれ、もう30巻ぐらい修めてくれています。たいへんな努力家です。
さて、H君に「すごいな~!」と私が思ったことは、6年生のK君、U君とはまた違うところに着目したことでした。もちろんH君が知るはずもなく、偶然なのでしょうが、私にはそれが驚きでした。なぜなら、U君がしようとしていて、時間がなくて断念した研究を補完するものだったからです。
H君は、1回ひねった輪(H君の用語では「ひねる=半回転」です)だと、真ん中で切ると、つながった輪ができるのに、2回ひねった輪(つまり1回転)だと、同じように切っても、輪が2つになることが、一番不思議だと感じたようでした。
そこで、H君はひねる回数を変化させて調べ出しました。そして、そのようなことがなぜ起こるかについて、次のような予想を立てました。
予想 奇数(1、3、5、7…)などは、ひねったらつながる。(まま)
つまり、1回ひねり(メビウスの輪)、3回ひねり、5回ひねり…と、奇数回ひねってつなげた輪は、半分にすると、つながったままの輪ができるはず、というわけです。そして、偶数回の場合は、2つの輪になる、と。奇数・偶数を自分の言葉として手の内に入れているようで、それも感心しました。H君はまた、奇数回の時はつなげる時に色が違う面が合わさる(表と裏がつながる)ことにも気付いていました。
さて、1回、3回ひねりについてまず実験してみて、それをスケッチに取りました。
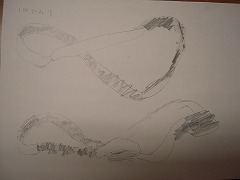
(上の図が1回ひねりの輪を半分に切ったあとの輪。つながっています)

(3回ひねりを切った輪。やっぱりつながっています)
ここまでは、確かに予想と同じでした。さて、次に5回ひねりを調べるか、それとも逆に2回ひねりを調べるか…。「2回の方がいいんとちがう?」と、H君。では、ドキドキのその場合を調べてみましょう。予想では、2つの輪になってほしいのですが…。

(2回ひねりを切った輪。おお!ちょっと見えにくいですが、ちゃんと2つに切れています。ということは、やはり奇数偶数には意味があるということで間違いない…?)
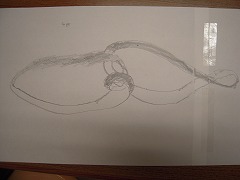
(念のため4回ひねりについても。これも輪が2つになりました)
1、3回ひねり…半分に切ると、つながった輪ができる
2、4回ひねり…半分に切ると、2つの輪ができる
ここまで予想通りとは、すごいです。ということは、ドンピシャだったというわけでしょうか。H君が最初に「偶数奇数」に着目したことが、ますます光ってきました。
H君がスケッチを描いているのを見ながら思ったことですが、今日はまるで発掘現場で、新種の化石を発見する人のような気持ちでした。「博士、これは新しい輪でしょうか?」と。H君が博士で、私はその助手です。(ことばのクラスでH君の書いた物語がちょうどそのような話だったので、そんな乗りになりました^^)
時間がきてしまったのが惜しいぐらいで、家でもぜひ5、6、7回ひねりのデータも取ってきてもらうように頼みました。H君のスケッチはいい味を出しているので、ぜひ加えてほしいです。でも実は、それが予想通りだったとしても、まだ「すべての」奇数について成り立つとは言えません。もしかしたら101回目のひねりの輪では、予想と違うことが起こるかもしれないのです。その可能性をなくすためには、今度は理屈を書くことが必要になってきます。こうなっているから必ずこうなると。それで一網打尽にできます。
「それができたらいいなあ」とH君。もちろん期待しています、博士!
この日の取り組みも「永久保存版」ですね(^^) スケッチも博士が描いたものなのですね。気持ちがこもっているのが伝わってきます。