かず５年

筆算だとなぜ、
　　　＿＿　　　　　　＿＿＿
0.2 ）12　　　が、　2）120　にするのか、その説明はいたって簡単です。それは、12÷0.2＝120÷2＝60とした方が計算しやすいという理由からです。筆算にすると、この10倍という作業が見えにくいのですが、式だと一目で分かります。

このことを一回確認しておけば、あとは学校で習ったとおり機械的に（おそらくそれが以前は気持ち悪かったのでしょう）、割り算の小数点は「右に動かす」と覚えておけば良いです。

H君はそれが納得できていたので、あとは計算間違いがないようにするだけでした。わざといじわるをした10÷0.01のような計算でも、間違わずに小数点を答が大きくなる方に移動させていたので安心です。以前自分で言っていた苦手意識は、どうやら克服されつつあるように見受けました。

後半は、時々このクラスでは工作の要素を取り入れています。以前は『ムービングキューブ』（Youtubeの動画が一見の価値ありです）というものを作ったので、今回は『ヘキサフレクサゴン』というものを作りました。

（H君作。平面の中から、不思議ふしぎ、３つの面が交互に現れてきます）

これについての詳しい説明は、このサイトが元ネタなので、そちらに譲ります。

製作には正三角形をたくさん描く必要があって、ひさびさにコンパスと定規を使いました。それでどうやったら正三角形が描けるか？─　これが４年生の時の復習になりました。

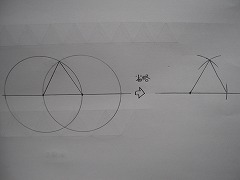
正三角形を描く時は、最初のうちはぜひ円を弧だけでなく「完全に描くこと」をおすすめします。（私が小学生の頃はなぜ描けるのかずっと不思議だったので…）H君にも正三角形になる理屈もたずねてみたところ、自分の描いたものを見ながら「三角形の三つの辺がどれも二つの円の半径で、その円の半径は同じ長さだから」と返ってきました。その通りです。これも割り算の小数点と同じで、一度納得しておけば、あとは問題なく描き方だけを覚えておけます。

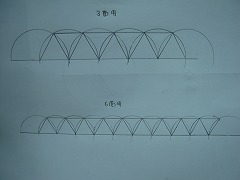
（フレクサゴン・３面と６面の設計図）

３面のフレクサゴンに挑戦したのですが、簡単にできそうに思いながら、正直、手こずりました。というのは、私がちゃんと説明を読んでいなかったせいなのですが…^^;。最後の貼り方（輪のつなげ方）を間違えるとうまくいかないことが、よくよく分かりました。H君は器用で私よりもきれいに作っていました（^^;）。

それで、いつか作ってみたいのですが、実はもっと多くの面を（６面、８面…何面でも）その中に閉じ込められます。私はまだ実物を一度も作れていません。完成したら、H君に見せたいと思います。

帰りしなにH君から「『分数の巻』作っておいて～！」というリクエストがありました。今日小数をしたからなのでしょう。次の展開を自分から言い出してくれるなんて、願ってもないことです（^^）ぜひ作っておきます。