かず６年（その１）

＜作り方＞
　
まず、筒を用意します。そして筒の中に筒を通して、最後に筒の内側と外側とを貼り付ければ完成。でも、3次元の世界だと、筒の中には筒は通せない（壁がぶつかる）ので、そこは「4次元を通って」という解釈で、本当は存在しない穴を開けます。

　
筒の中に筒を通します（この穴は、四次元を通ることを意味します）。そして最後に上で筒の縁を裏返して、内側（白）と外側（紫）とをはり合わせれば、壷が完成。長靴みたいですね。

　
さて、ここからがマジック。この壷をメビウスの輪の時と同じように、壷の容器の部分を、真っ二つにじょきじょき切っていきます。するとどうなるでしょうか…？
「普通の紙に戻るんとちがう？」「いやきっとこれと同じ壷が二つできるんや」「そうか！ きっとそうやな」
さてさて…あれれ？ そうこうするうちに、何やら２つの破片が出てきましたが、これを丁寧に広げてみると…。

「おお～！」「これって、どっちもメビウスの輪や！」
二人とも心を動かされたようです。さっそく、二人にも作ってもらいました。（紙だと破れやすいので、材質を変えてみました）

　
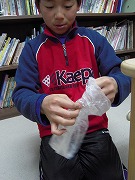
Ｋ君は傘入れのビニールで作成。
「先を、引っ張り出して…」「裏返してとめる…と。これ透明やから分かりやすいぞ」と、どうやら気に入ってくれたようです（^^）

Ｕ君は、すべり止めマットで。
「ここらへんに、穴を開けて…」「わあ、手が吸い込まれる～」　

「持ってるで」「あ！ ありがとう」

　
Ｋ君の『クラインの壷』完成。「サイコロを中でころがしてみよう」

　
Ｕ君のも完成。それぞれで実験。

さてサイコロを使って確認したところ、サイコロは最初の壷の入り口を「外側」（白い面でくるんだ穴）から入って、最後に壷の入り口の「内側」（紫の面でくるんだ袋小路）」に出てきました。場所的には同じスタート地点に戻ってきたわけですが、その時、世界の表と裏が違います（これがポイントです）。

このことは、実はメビウスの輪でも起こっていて、表側のスタート地点から出発して一周してくるとスタート地点の裏側に来るのと同じ現象だ、という説明をしました。

「そうか。だってメビウスの輪も、作るときに色の違う面をはり合わせてるもんなあ。これ（壷）だってそうだったし。入り口と出口を裏返してはってたから、同じことが起こったんや」と、口々に言うK君とU君。二人の頭の中で、何やらぴかっと「見えた」ようです。

＃ちなみに『幾何学』というのは、「それが『何』であるかを『幾』（み）る学問」のことです。（また「『それ』が分かった！」時の喜びを「形相悦」というそうで、K君とU君の味わったのもまさにそれだったでしょう）

この壷（クラインの壷といいます）を切ると、メビウスの輪が２つできたということは、逆に平べったいメビウスの輪を重ねることで膨らませ、立体的にすると、壷ができあがる、と言うわけです。つまりこれがメビウスの輪の立体版である、と確認できました。

二人が作っている頃、私はみかんの網で…うーん、しょぼいできです^^;